Phương pháp chọn mẫu theo xác suất gồm có 4 phương pháp sau:
- Chọn mẫu theo phương pháp ngẫu nhiên đơn giản
- Chọn mẫu theo phương pháp hệ thống
- Chọn mẫu theo phương pháp phân tầng
- Chọn mẫu theo phương pháp chọn theo nhóm
1. Chọn mẫu theo phương pháp ngẫu nhiên đơn giản: Là phương pháp chọn mẫu hoàn toàn ngẫu nhiên, không theo một sự sắp xếp nào cả. Các đơn vị đều có cơ hội được chọn như nhau.
Ví dụ: Một trường học có 1.000 sinh viên, người nghiên cứu muốn chọn ra 100 sinh viên để nghiên cứu về tình trạng sức khỏe trong số 1.000 sinh viên. Theo cách chọn mẫu đơn giản thì chỉ cần viết tên 1.000 sinh viên vào trong mẫu giấy nhỏ, sau đó bỏ tất cả vào trong một cái thùng và rồi rút ngẫu nhiên ra 100 mẫu giấy. Như vậy, mỗi sinh viên có một cơ hội lựa chọn như nhau và xác suất chọn ngẫu nhiên một sinh viên trên dễ dàng được tính. Thí dụ trên ta có quần thể N = 1.000 sinh viên và cỡ mẫu n = 100 sinh viên. Như vậy, sinh viên của trường được chọn trong cách lấy mẫu ngẫu nhiên sẽ có xác suất là n/(N x 100) hay 100/(1000 x 100) = 10%.
• Trong phương pháp này các phần tử đều có xác xuất tham gia vào mẫu như nhau và biết được trước.
• Ưu điểm: đơn giản, dễ thực hiện nếu có một khung mẫu hoàn chỉnh, cho kết quả khách quan.
• Nhược điểm: mức phân bố mẫu trên đám đông có thể bị vi phạm nhất là đám đông nghiên cứu có kích thước lớn và kích thước mẫu nhỏ. Phải xây dựng dàn chọn mẫu liệt kê đầy đủ tất cả các phần tử của tổng thể, nếu tổng thể chung có quy mô lớn thì việc chuẩn bị này tốn nhiều thời gian và hết sức khó khăn.
• Phạm vi sử dụng: chỉ có thể sử dụng phương pháp này trong các trường hợp đám đông có kích thước nhỏ và thường được sử dụng cho việc chọn phần tử cho các phương pháp chọn mẫu khác như chọn điểm xuất phát trong phương pháp hệ thống. Chỉ ứng dụng phương pháp này trong trường hợp tổng thể nghiên cứu tương đối đồng chất, không bao gồm nhiều loại hình khác nhau.
• Ví dụ: ta có thể sử dụng lệnh Rand (random) trong excel để chọn ngẫu nhiên các phần tử
2. Chọn mẫu theo phương pháp hệ thống/ chọn mẫu ngẫu nhiên máy móc:
Là phương pháp chọn ngẫu nhiên trong điều kiện các đơn vị chọn mẫu trong dàn chọn mẫu được sắp xếp theo một trật tự nhất định
• Trong phương pháp này nhà nghiên cứu sắp xếp kích thước N của đám đông theo thứ tự từ 1 đến N. Sau đó tính bước nhảy SI = N/n, đây là tỷ lệ chọn mẫu. Sau đó chọn ngẫu nhiên một điểm xuất phát, và không nhất thiết phải bắt đầu bằng nhóm đầu tiên mà có thể thực hiện ở bất kỳ nhóm nào trước.
• Ưu điểm: khắc phục được khả năng phân bố không đều của phương pháp ngẫu nhiên đơn giản
• Nhược điểm: nếu khung mẫu được xếp theo chu kỳ và tần số của nó trùng với bước nhảy thì mẫu sẽ bị chệch. Bổ sung: Khó khăn khi lập dàn chọn mẫu trong trường hợp tổng thể lớn.
• Phạm vi sử dụng: có thể sử dụng cho tất cả các mẫu cần nghiên cứu
• Ví dụ: chọn mẫu có kích thước n = 100 trong một đám đông có kích thước N = 1000. Bước nhảy sẽ là SI = 1000/100 = 10. Để chọn phần tử đầu tiên trong các phần tử từ 1 đến 10, chúng ta dùng phương pháp chọn ngẫu nhiên đơn giản. Giả sử chọn được phần tử thứ 6 thì lúc này phần tử thứ hai tham gia vào mẫu là phần tử thứ 16 (6 + 10), phần tử thứ 3 sẽ là 26 (16 + 10)… như vậy phần tử thứ 100 tham gia vào mẫu sẽ là 996.
3. Chọn mẫu theo phương pháp phân tầng/ chọn mẫu ngẫu nhiên theo cụm
• Trong phương pháp này người ta chia đám đông ra làm nhiều nhóm nhỏ, các nhóm này chính là đơn vị chọn mẫu. Các nhóm này thỏa mãn tiêu chí là các phần tử trong cùng một nhóm có tính đồng nhất và các phần tử giữa các nhóm có tính dị biệt. Các nhóm này cũng có thể được chia thành nhiều nhóm nhỏ hơn nhưng cũng cần phải thỏa mãn tiêu chí trên. Để chọn từng mẫu cho các nhóm, chúng ta sẽ phải sử dụng phương pháp hệ thống hoặc ngẫu nhiên đơn giản.
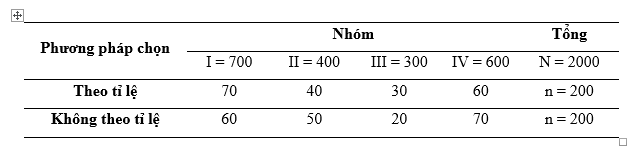
• Phương pháp chọn mẫu phân tầng có thể được thực hiện theo tỷ lệ (số lượng phần tử chọn cho mẫu trong từng nhóm tỷ lệ với số lượng phần tử của chúng) hoặc không theo tỷ lệ (số lượng phần tử chọn cho mẫu trong từng nhóm không tỷ lệ với số lượng phần tử của chúng)
• Ưu điểm: cho hiệu quả thống kê cao nhất, mẫu chọn có tính đại diện cao..
• Nhược điểm: cần phải phân nhóm trước và yêu cầu các phần tử trong đám đông cần phải có tính đồng nhất cao. Gặp khó khăn trong việc xác định cơ cấu tổng thể (không có thông tin trong quá khứ)
• Phạm vi sử dụng: có thể sử dụng cho tất cả các mẫu cần nghiên cứu/ Chỉ ứng dụng khi tiêu thức phân tổ có cơ cấu tương đối ổn định.
• Ví dụ:
4. Chọn mẫu theo phương pháp chọn theo nhóm
• Nhà nghiên cứu cũng chia đám đông ra thành nhiều nhóm nhỏ như trong phương pháp phân tầng. Tuy nhiên, các nhóm này có đặc điểm là các phần tử trong cùng nhóm có tính dị biệt cao và các phần tử giữa các nhóm có tính đồng nhất cao. Các nhóm này cũng có thể được chia thành nhiều nhóm nhỏ hơn nhưng cũng cần phải thỏa mãn tiêu chí trên. Để chọn từng mẫu cho các nhóm, chúng ta sẽ phải sử dụng phương pháp hệ thống hoặc ngẫu nhiên đơn giản.
• Trong phương pháp này chúng ta phải chọn đơn vị nhóm thay vì chọn phần tử như các phương pháp khác. Nếu chọn theo cách thức này thì nó được gọi là chọn theo nhóm một bước.
• Nếu sau khi đã chọn được nhóm, chúng ta lại tiến hành chọn phần tử trong từng nhóm để tham gia vào mẫu thì phương pháp chọn mẫu theo nhóm dạng này được gọi là phương pháp chọn mẫu theo 2 bước. Do đó, tương tự như vậy chúng ta sẽ có thể chọn mẫu theo nhóm ba bước …
• Ưu điểm: thích hợp với các đám đông nghiên cứu chưa có khung mẫu hoàn chỉnh cho cả đám đông, mà chỉ cần khung mẫu cho nhóm đã chọn (nếu chỉ chọn các phần tử trong nhóm).
• Nhược điểm: hiệu quả thống kê của phương pháp này rất thấp vì việc chia nhóm để thỏa mãn nguyên tắc cùng nhóm dị biệt, khác nhóm đồng nhất là rất khó khăn do các phần tử gần nhau (trong nhóm) thường có tính đồng nhất cao.
• Phạm vi sử dụng: hạn chế do khó khăn trong việc chia nhóm.
• Ví dụ: giả sử chúng ta muốn chọn mẫu có kích thước n = 200 từ một đám đông có kích thước N = 2000 bằng phương pháp chọn mẫu theo nhóm. Chúng ta tiến hành chia đám đông này thành các nhóm (giả sử 20 nhóm) và chọn ngẫu nhiên 10 nhóm để nghiên cứu. Sau đó ta có thể dùng phương pháp hệ thống để chọn 200 phần tử cho mẫu từ mười nhóm trên.
